相信大家都知道二分搜索，在一个有序的列表中，使用二分搜索，能够以O(logN)的时间复杂度快速确定目标是不是在列表中。

二分搜索的代码非常简单，使用递归只需要几行代码就能搞定：

def binary_search(sorted_list, target):
    """
    sorted_list是单调递增的列表
    """
    if not sorted_list:
        return False
    mid = len(sorted_list) // 2
    if target > sorted_list[mid]:
        return binary_search(sorted_list[mid + 1:], target)
    elif target < sorted_list[mid]:
        return binary_search(sorted_list[:mid], target)
    else:
        return True

运行效果如下图所示：

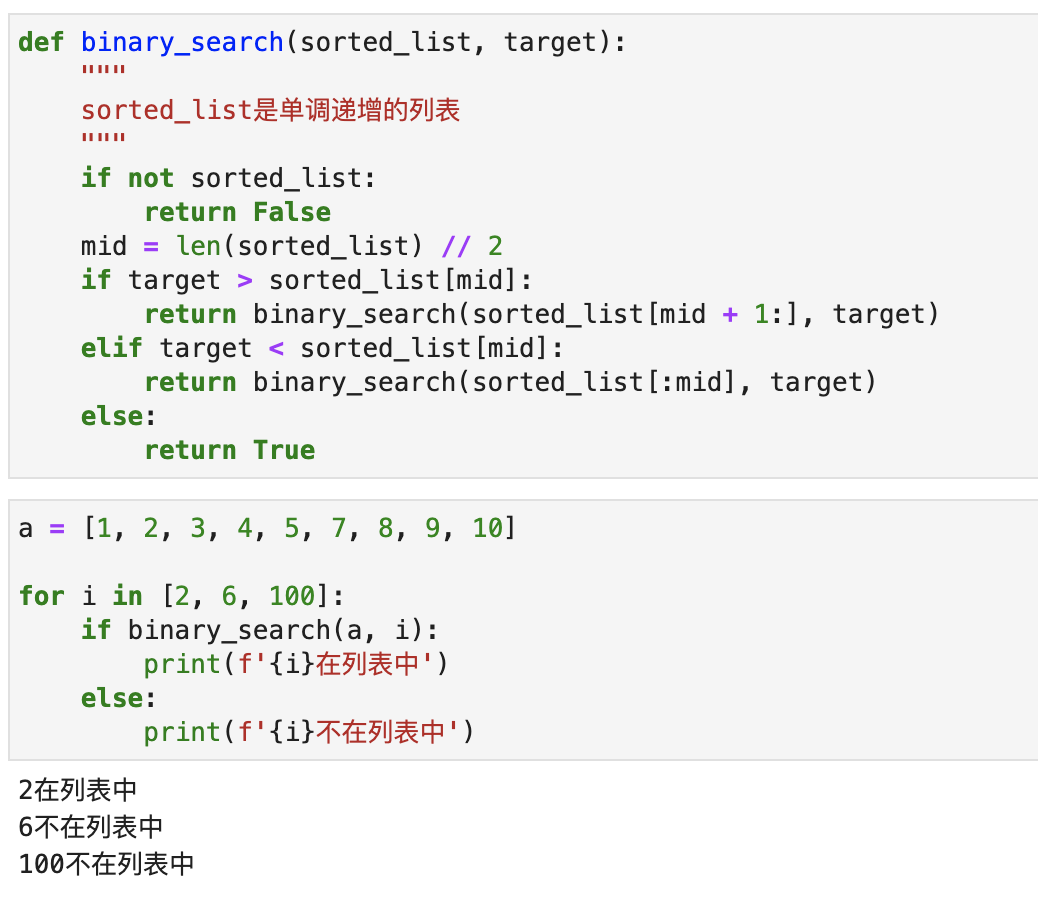
Python自带了一个二分搜索的模块，叫做bisect，它也能实现二分搜索，但是它的执行结果跟我们上面代码的效果有点不同：

import bisect

a = [41, 46, 67, 74, 75, 76, 80, 86, 92, 100]
index = bisect.bisect(a, 75)
print(index)

index = bisect.bisect(a, 82)
print(index)

运行效果如下图所示：

可以看到，bisect.bisect()返回一个索引。如果要搜索的数已经在列表里面了，那么它返回的是这个数在列表中，最右边的这个目标数的索引+1. 以列表[41, 46, 67, 74, 75, 76, 80, 86, 92, 100]为例，要搜索75。由于75在原来列表中的索引是4。因此返回索引+1也就是5. 如果原来列表中，75出现了多次，比如[41, 46, 67, 74, 75, 75, 76, 80, 86, 92, 100]那么返回的是最右边那个75对应的索引+1，也就是6。

如果要找的数字不在原来列表中，那么bisect.bisect()会返回一个索引，当我们把目标数字插入到这个列表中对应索引的位置时，列表依然有序。例如[41, 46, 67, 74, 75, 76, 80, 86, 92, 100]中，我们找82。它返回的是7。原来列表里面索引为7的位置是数字86，我们把82插入到这个位置，原有的数据依次后移一位，此时列表依然有序。

bisect这个模块还有一个函数，叫做bisect.bisect_left()。如果目标数字在原来的列表中，那么返回的是最左边那个数字对应的索引.如果不在列表中，那么返回的索引插入目标数字以后依然有序，如下图所示：

这个函数看起来非常简单，但你可能不知道，它在分布式系统中也有重要的用途。

假设现在你有10个Redis的单节点用来做分布式缓存。因为某种原因，你不能做集群。当你要搜索一个数据的时候，你要先确定这个数据在不在Redis中。如果在，就直接从Redis中读取数据；如果不在，就先去数据库里面读取，然后缓存到Redis中。

因为数据量很大，你不能把同一份数据同时存在10个Redis节点里面，因此你需要设计一个算法，不同的数据存放在不同的Redis节点中。

当你要查询数据的时候，你能根据这个算法查询到数据（如果在缓存中）应该存放在哪个Redis中。

稍微有一点分布式系统设计经验的同学肯定会想到，这个简单啊，10个Redis节点编号0-9.对key计算Hash值，这个哈希值是32位的十六进制数，可以转换成十进制以后对10求余数，余数是多少，就放到对应的节点里面。

这样一来，只要来了一个新的数据，你只需要去余数对应的Redis中判断它有没有缓存就可以了。

但问题来了，如果你开始使用这个方法，Redis中已经有数据了，那么你的Redis节点数就不能变了。一旦你增加或者减少1个节点，所有余数全部变了，新来的数据找到的Redis节点肯定是错的。例如key的Hash值原来除以10，余数是2，现在除以9，余数是1.那本来你应该去2号Redis找缓存，现在却跑到1号Redis找缓存，那一定找不到。

这个问题要怎么解决呢？我们用一个简单的例子来做演示。假设我现在有一个列表：[200, 250, 300, 400, 500, 530, 600]。每个数字代表这个价位的房子。单位是万。你想买一个房子，但便宜的房子太破，好的房子又太贵。因此你只找价格等于你的期望，或者虽然比你的期望略高但差距最小的房子。

假设现在你的期望是250万，而正好有个房子卖250万，因此你可以买它。

假设现在你的期望是470万，那么你唯一的选择是500万的房子。

到目前为止应该非常好理解，那么我们来增加或者减少候选项：

1. 500万的房子被别人买走了。列表变成[200, 250, 300, 400, 530, 600]，因此唯一适合你的是530万的房子。
2. 如果现在250万的房子被人买走了，列表变成[200, 300, 400, 500, 530, 600]。此时对你没有任何影响，适合你的房子还是500万的房子。
3. 如果现在增加了一个480万的房子，列表变成[200, 250, 300, 400, 480, 500, 530, 600]。那么现在适合你的房子变成了480万。
4. 如果现在增加了一个240万的房子，列表变成[200, 240, 250, 300, 400, 500, 530, 600]。此时对你没有任何影响，适合你的还是500万的房子。

这个场景，我们正好可以使用bisect.bisect_left()！效果如下图所示：

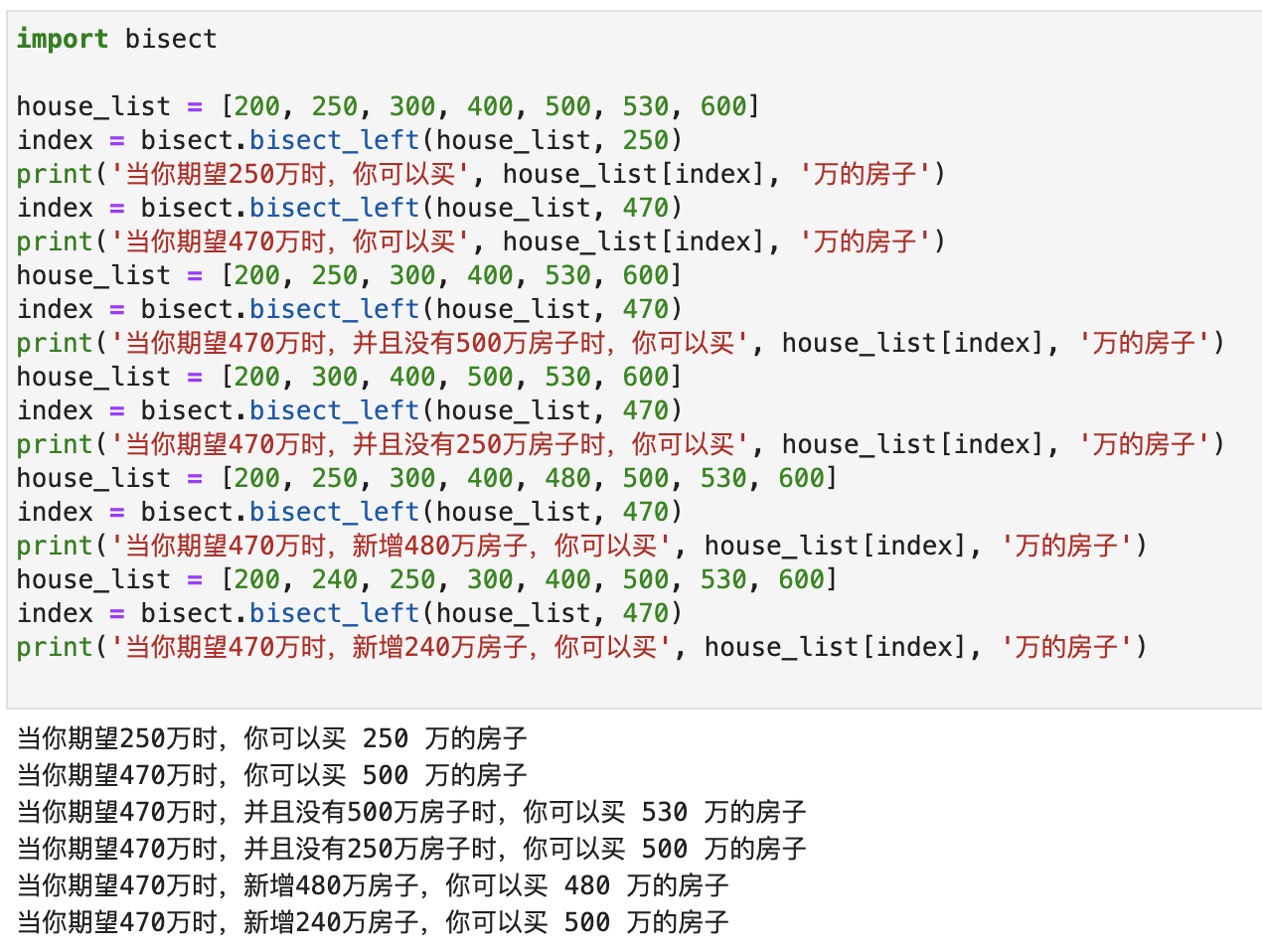
当备选项发生改变的时候，只有你目标选项附近的房子受到了影响。而小于你候选项的房子和贵的多的房子的变动，对你没有任何影响。

你注意到了吗，这个场景跟我们分布式缓存增减Redis节点的场景非常像。我们原来有10台Redis，现在新增了一台，变成11台了。那么只有一台Redis的部分缓存会迁移到这个新增的Redis中。而其它9台Redis的缓存不需要做任何改变。

同理，当我们删除一台Redis节点时，这个被删除的节点里面的数据，只需要同步到它旁边的另一台Redis节点中就可以了。另外8个Redis节点不需要做任何修改！（也可以不同步，只有一小部分key会因为删除这个节点导致找不到数据，而重新读数据库。80%的缓存不会受到任何影响。）

这就是一致性Hash的算法。

我来简单描述一下这个算法的实现过程。首先，我们使用redis.Redis(不同redis的连接参数)创建10个连接对象。然后把每个连接对象和一个Hash值创建映射，如下图所示：

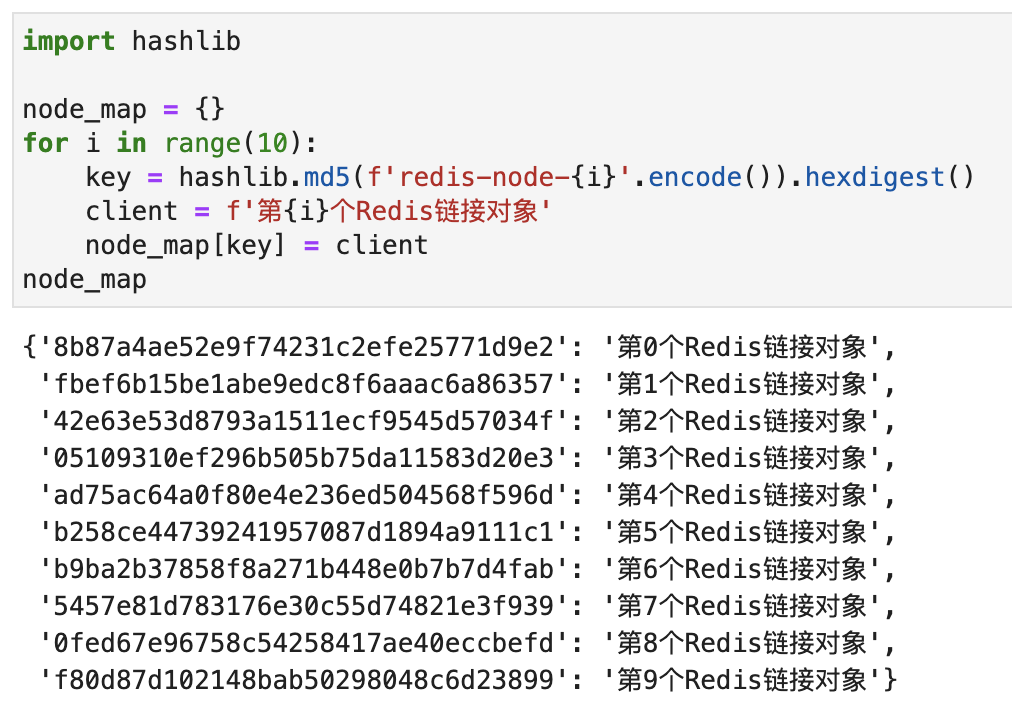
然后，我们把这10个Hash值排序以后放到一个列表中。如下图所示：

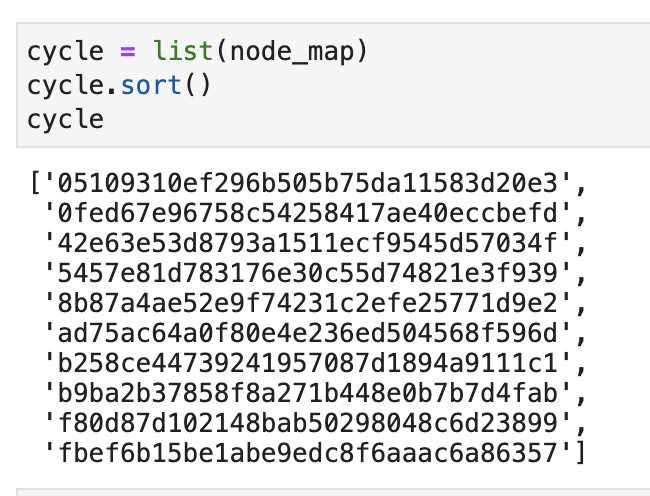
现在，来了一条新的缓存查询需求，我们计算key对应的Hash值，然后使用bisect.bisect_left()到列表中去寻找它对应的Redis节点的Hash值的索引。如果返回的索引等于列表的长度，那么让索引等于0. 找到索引以后，拿到对应的Redis节点的Hash，最后再用这个Hash去找到对应的Redis节点，简化代码如下：

`

如果新增或者删除了Redis节点，那么只需要更新node_map和cycle就可以了。只会发生很小的数据迁移，对绝大部分的缓存都不会造成任何影响。例如我现在把第1个Redis链接对象对应的Hash：fbef6b15be1abe9edc8f6aaac6a86357从node_map和cycle中删除。再进行查询，会发现依然找到的是编号为6的Redis节点。

一致性Hash在分布式系统中有广泛的应用。但你可能想不到，它的核心原理就是二分搜索里面的bisect_left。

当然，上面只是简化算法。一致性Hash的完整算法还涉及到虚拟节点和避免数据倾斜的算法。如果大家有兴趣的话，我也可以写一篇文章，完整解释它的算法实现。