上篇讲了个如何使用gpu.js这个库来进行简单的gpu计算虽然简单易用但是本身的局限也很多目前这个库也不是非常完善有待改进那咱就从原理开始来自己搞一个吧当然并不是指实现一个这个的通用的库而是使用相关原理完成一个是用GPU计算的demo 当然还是矩阵的乘法

前端使用GPU的能力是通过webgl实现的更加广泛的理解的可以认为是通过canvas来说实现的 canvas估计对大多数前端来说并不陌生 canvas有许多个像素组成每个像素的颜色可以有RGBA四个维度表示每个维度范围为0-255 既8位把RGBA表示成数值的话那每个像素可以存32位这就是前端使用gpu计算最为核心的一点每个像素可以存储一个32位的值, 刚刚好就是一个int或者uint

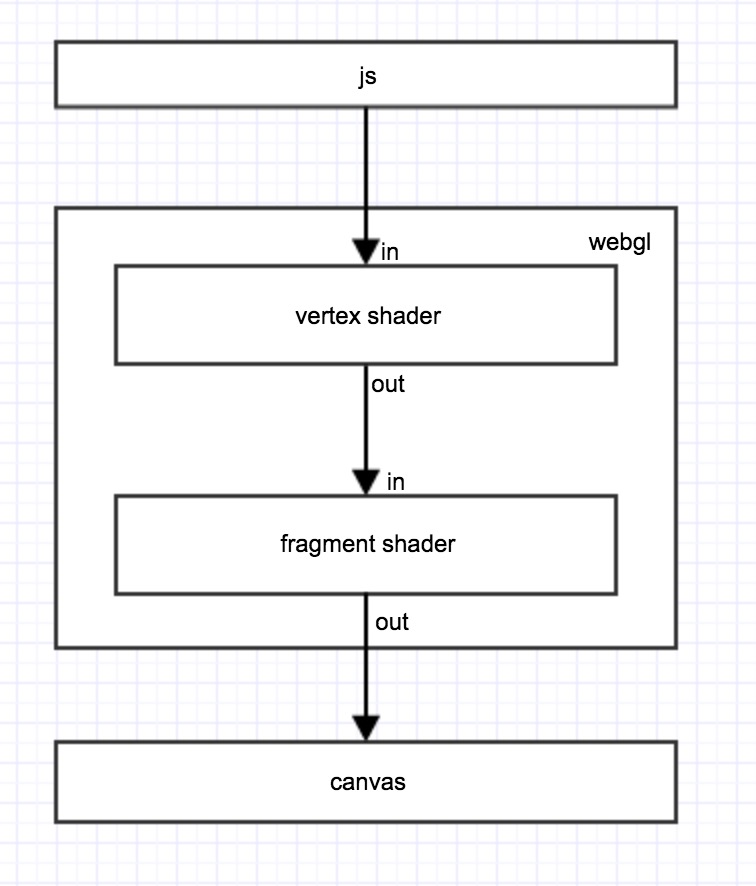
0.基本WebGL绘制

首先从最简单的绘制一个图像开始 webgl绘图的流程最简单的就这样

其中两个vertex shader和fragment shader为两个GLSL代码片段分别处理坐标数据和颜色数据 vertex shader和fragment shader的执行是以像素为单位

canvas开始绘制的时候 vertex shader中得到每个需要绘制的像素的坐标视需要可以对坐标进行各种转换最终得到一个最终位置这个过程中可以将数据作为输出传入fragment shader 参与下一步的计算

fragment shader接受各种输入最终输出一个RGBA颜色数据作为该像素点的颜色值

当所有像素都绘制完成之后画布绘制完成

0.0 js中的流程就比较简单了

创建webgl program
初始化两个shader
传入各个顶点坐标
开始绘制

因为咱们主要是计算所以对坐标相关的数据可以不用太多关注咱们直接画一个铺满画布的矩形就可以了

// 加载资源
async function loadRes(file) {
    const resp = await fetch(file);
    return resp.text();
}

const canvas = document.querySelector("canvas");
const gl = canvas.getContext("webgl2");
const program = gl.createProgram();

// 载入shader
function initShader(code, type) {
    const shader = gl.createShader(type);
    gl.shaderSource(shader, code);
    gl.compileShader(shader);
    if (!gl.getShaderParameter(shader, gl.COMPILE_STATUS))
        throw new Error("compile: " + gl.getShaderInfoLog(shader));
    gl.attachShader(program, shader);
}

// 获取attribute参数的地址
function getAttribLoc(name) {
    const loc = gl.getAttribLocation(program, name);
    if (loc == -1) throw `getAttribLoc  ${name} error`;
    return loc;
}


async function startDraw(vertexShader, fragmentShader) {
    // 加载shader的代码
    const vshaderCode = await loadRes(vertexShader);
    const fshaderCode = await loadRes(fragmentShader);

    // 载入shader
    initShader(vshaderCode, gl.VERTEX_SHADER);
    initShader(fshaderCode, gl.FRAGMENT_SHADER);
    
    gl.linkProgram(program);
    gl.useProgram(program);

    // 传入坐标信息 具体含义后有说明
    gl.bindBuffer(gl.ARRAY_BUFFER, gl.createBuffer());
    const vecPosXArr = new Float32Array([-1, -1, 1, -1, -1, 1, 1, 1]);
    gl.bufferData(gl.ARRAY_BUFFER, vecPosXArr, gl.STATIC_DRAW);
    
    // 将顶点信息绑定到vertex shader中的变量  以两个数值作为一组数据
    // 所以上述8个数值实际标明了4个顶点坐标
    // g_pos为vertex中的自定义的变量名
    const posAtrLoc = getAttribLoc("g_pos"); 
    gl.enableVertexAttribArray(posAtrLoc);
    gl.vertexAttribPointer(posAtrLoc, 2, gl.FLOAT, false, 0, 0);
    
    // 清理画布
    gl.clearColor(.0, .0, .0, 1);
    gl.clear(gl.COLOR_BUFFER_BIT);
    
    // 使用4个坐标连续绘制两个三角形
    gl.drawArrays(gl.TRIANGLE_STRIP, 0, 4);
}

需要注意的一点vertex shader中得到的坐标是以canvas中心为(0,0) 水平向右为x轴正方向垂直向上为y轴正方向两轴的取值范围为[-1, 1] 所以上面js代码中传入的顶点坐标范围为[-1, 1]的浮点数

另外OpenGL中绘制面都是以三角形为单位的 webgl中也不例外提供了一个绘制连续三角形的方式一个矩形是两个三角形所以传入四个顶点就可以了当然也可以传入六个顶点分别绘制两个三角形

顶点的传入实际上是传入一个数组然后vertexAttribPointer()方法指定各个顶点如何使用这个坐标数组可以认为是8个一维坐标也可以认为是2个二维坐标或者是2个四维坐标所以上述的例子实际是传入了4个2维坐标

接下来就是两个shader中的流程目前大部分浏览器已经支持WebGL 2.0标准对应OpenGL ES 3.0 所以shader中的语法需要遵循相关语法

具体的版本可以使用gl.getParameter(gl.SHADING_LANGUAGE_VERSION)获取

0.1 首先`vertex shader`:

#version 300 es

precision highp float;
precision highp int;

in vec4 g_pos;
out vec2 v_pos;

void main() {
    float curX = (g_pos.x + 1.) / 2.;
    float curY = (g_pos.y + 1.) / 2.;
    v_pos = vec2(curX, curY);

    gl_Position = g_pos;
}

具体的语法啊变量类型啊什么的可以看官方的文档

只做一点说明 in将变量标记输入 out将变量标记输出在webgl 1.0中 attribute表示输入所以在js获取变量地址的时候使用了getAttribLocation函数其中的Attrib即是这个意思但是在webgl 2.0这个声明被弃用使用in来代替

out标记的变量的值将作为fragment shader的输入

gl_Position为内部变量作为最终的坐标地址实际中还有很多其他内置变量就不举例了

上述的代码将以画布中心为原点的坐标系转化为以左下角为原点的坐标系并将新的坐标系中的坐标传给下一步后续会解释为什么要做这样一个坐标变换

0.2 然后就是`fragment shader`:

#version 300 es

precision highp float;
precision highp int;

in vec2 v_pos;
out vec4 o_result;

void main() {
    float pos_x = v_pos.x;
    float pos_y = v_pos.y;

    float distance = sqrt(pos_x * pos_x + pos_y * pos_y);

    o_result = vec4(1, 0, 0, 1. - distance);
}

同样 fragment shader中也有in和out关键字

其中in对应vertex shader中的 out 变量类型以及变量名必须一致

out为一个vec4类型存放最终的RGBA结果每个值的范围为[0, 1]

上述的代码也很简单颜色固定为红色但是透明度按照像素到原点的距离递增距离越远透明度越高

最终画出的效果是这样的

1.输入

上面已经讲了一个坐标的输入但是计算相关的参数需要其他的方式传入需要一点提醒由于js中的所有数值都是浮点型所以js和webgl进行数据传输的时候 全都必须使用类型数组 并且相当多函数只能接受某种特定的类型数组

1.0 粗暴的替换

因为两个shader都是js获取到的资源所以在载入webgl之前可以对内容进行直接修改

一般来说 shader中要获取canvas实际的大小相当不便所以可以直接用这个办法将画布大小传入

js中:

1	fshaderCode = fshaderCode.replace(/CANVAS_SIZE/g, canvas.width);

shader中:

1	const int U_LENGTH = CANVAS_SIZE;

这样可以直接在其他地方获取画布大小了不过这个方法得保证不会替换错了

最重要的是这个办法对传入数据的格式非常有限

1.1 使用 uniform 关键字

这个方法就比较强大了不仅一般的int／float 还可以传入向量数组矩阵等各种类型

而且两个shader可以共享同一份数据

function getUniformLoc(name) {
    const loc = gl.getUniformLocation(program, name);
    if (loc == null) throw `getUniformLoc ${name} err`;
    return loc;
}
const uniLoc = getUniformLoc("i_matrixA");
gl.uniform1fv(uniLoc, new Float32Array([1, 2, 3, 4]));

shader中:

1	uniform float i_matrixA[4];

uniform()是个一系列的方法传入不同类型的时候使用了不同的函数比如上面的uniform1fv以及后面的uniform1i 详细了解还是得看文档

这个方法等好处就是支持所有类型但是也有一个问题不过这个问题并不算是uniform的问题而是WebGL本身的局限:

数组长度受限, 可以使用gl.getParameter(gl.MAX_FRAGMENT_UNIFORM_VECTORS)或者gl.getParameter(gl.MAX_VERTEX_UNIFORM_VECTORS)获取数组长度上限本人实测值为1024
OpenGL ES 3.0不支持多维数组, 这个问题将在下个版本中得到支持, 当前情况还是无解

当然还有第三种方法解决大量数据传入的问题

1.2 使用Texture 纹理

纹理就是另外的图案这个就不多做解释了说白了就是另外一副图因为图都是由像素构成的所以可以用纹理来传入大量的数据

function initTexture(index, tSampler, pixels) {
    const texture = gl.createTexture();
    gl.activeTexture(gl[`TEXTURE${index}`]);
    gl.bindTexture(gl.TEXTURE_2D, texture);

    gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER, gl.LINEAR);
    gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MAG_FILTER, gl.NEAREST);

    gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA, dimen, dimen, 0,
        gl.RGBA, gl.UNSIGNED_BYTE, pixels, 0);
    gl.uniform1i(getUniformLoc(tSampler), index);
}
const colorMap = new Uint32Array([
    0xFF0000FF, 0x00FF00FF, 0x0000FFFF,
    0xFFFF00FF, 0xFF00FFFF, 0x00FFFFFF,
    0x000000FF, 0xFFFFFFFF, 0xF0F0F0FF,
]);
const RGBAMap = new Uint8Array(colorMap.buffer);
initTexture(0, "samplerA", RGBAMap);

纹理的定义有点复杂纹理的大小非常苛刻只能是2^n * 2^n的大小但是数据不可能是固定的所以这里有个纹理进行伸缩的过程

使用设置gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER, gl.LINEAR)来设置伸缩方式当然实际上这个对我们这个计算没有影响因为我们全程按百分比取值

除了缩放还有要定义未定义点的颜色规则比如3 * 3的图 1/6, 1/2, 5/6这三个位置的点和传入值完全一样这个没有问题但是其他位置默认是渐变
可以使用gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MAG_FILTER, gl.NEAREST)来设置不使用渐变即各个色块都是三等分关于两种效果下面有例子可以看

另外参数传入可以选择多种方式直接用<img>标签也可以或者直接传入像素值也可以具体方式可以查看texImage2D文档

当然传入透明的值也是可以的绘制到画布上的话真的是透明的相当神奇

但如果是像素值传入也可以有多种格式本例子中将RGBA拆开成四个值分别传入为了方便起见可以直接使用类型数组直接将32位转成8位但是这样的转化方式可能会引起顺序不一致比如[0x01020304] 会被拆成[0x04, 0x03, 0x02, 0x01] 具体相关内容可以参考类型数组

最后将纹理的索引绑定到纹理变量上注意到下面sampler2D类型其实也是int 这种类型被称为Opaque Types https://www.khronos.org/opengl/wiki/Data_Type_(GLSL)#Opaque_types 注意下就可以

shader 中:

uniform sampler2D samplerA;
void main() {
  vec4 color = texture(samplerA, v_pos);
  o_result = color.abgr;
}

texture()为内置函数用以获取某个纹理在某点的颜色

为了保持输入的时候rgba顺序一致在获取到纹理中某个值的时候需要重新调整顺序

关于纹理的坐标系和canvas的是不一样的是以左下角为原点水平向右为x正方向垂直向上为y轴正方向所以前面把canvas坐标进行转化也是为了和纹理的坐标系一致

另外像素写入的顺序也是是从左下开始先向右写入一行再依次向上写入每一行

然后直接将纹理的数据1:1对绘制到画布上的效果

默认使用渐变来获取各个颜色很明显有9个点是渐变的中心就是上面传入的那九个值了

设置了gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MAG_FILTER, gl.NEAREST)后九大块方块

对于计算中后者才是我们想要的效果不然取值还取到不认识的值计算要崩啊

使用Texture解决了要传入大量数据的问题但是使用比较复杂而且数据传输也是相当地耗时所以还是期待多维数组Arrays of Arrays#Arrays_of_arrays) 能早一天在浏览器上支持

2. 输出

输出的方式单一直接将值赋到fragmengt的out声明的变量上就可以将对应的值绘制到画布上接着可以使用gl.drawArrays()方法来读取各个像素上的点和纹理的输入一样读取像素的方法也有很多参数和重载为了方便咱们使用下面这种直接读取RGBA这四个维度的值

gl.drawArrays(gl.TRIANGLE_STRIP, 0, 4);
let picBuf = new ArrayBuffer(canvas.width * canvas.width * 4);
let picU8 = new Uint8Array(picBuf);
let picU32 = new Uint32Array(picBuf);
gl.readPixels(0, 0, canvas.width, canvas.width, gl.RGBA, gl.UNSIGNED_BYTE, picU8);
console.log(picU32);

注意 readPixels方法必须和drawArrays方法在同一个执行队列中同步执行否则会无法读取到数据

同上面输入的理这里使用了Uint32Array和Uint8Array进行数据转化 ArrayBuffer的长度即为画布的像素数量乘上4 因此在fragment中输出的时候需要反转四个维度

读取的顺序和纹理写入的顺一致都是从左下开始沿x正方向读取一行再向y方向读取各行最后合并成一个完整的数组如果输入输出和这个顺序有关的话需要注意一下

3. 矩阵乘法实验

好了搞了这么多已经吧基本的输入输出搞定了咱来开始试一下矩阵相乘吧

不多说了直接上代码

0. 先是一个基本类

包含了输入输出等基本方法以及会用到的其他方法基本上前面都有介绍

class GPUComputing {
    constructor(dimen, canvasSize) {
        this.dimen = dimen;
        this.canvas = document.createElement("canvas");
        this.canvas.width = canvasSize || dimen;
        this.canvas.height = canvasSize || dimen;
        this.gl = this.canvas.getContext("webgl2");
        this.program = this.gl.createProgram();
    }

    async init(vertexShader, fragmentShader) {
        const vshaderCode = await this.loadRes(vertexShader);
        let fshaderCode = await this.loadRes(fragmentShader);
        fshaderCode = fshaderCode.replace(/CANVAS_SIZE/g, this.dimen);

        this.initShader(vshaderCode, this.gl.VERTEX_SHADER);
        this.initShader(fshaderCode, this.gl.FRAGMENT_SHADER);

        this.gl.linkProgram(this.program);
        this.gl.useProgram(this.program);

        this.gl.bindBuffer(this.gl.ARRAY_BUFFER, this.gl.createBuffer());
        let vecPosXArr = new Float32Array([-1, -1, 1, -1, -1, 1, 1, 1]);
        this.gl.bufferData(this.gl.ARRAY_BUFFER, vecPosXArr, this.gl.STATIC_DRAW);

        let posAtrLoc = this.getAttribLoc("g_pos");
        this.gl.enableVertexAttribArray(posAtrLoc);
        this.gl.vertexAttribPointer(posAtrLoc, 2, this.gl.FLOAT, false, 0, 0);

        this.gl.clearColor(.0, .0, .0, 1);
        this.gl.clear(this.gl.COLOR_BUFFER_BIT);
    }

    initShader(code, type) {
        const shader = this.gl.createShader(type);
        this.gl.shaderSource(shader, code);
        this.gl.compileShader(shader);
        if (!this.gl.getShaderParameter(shader, this.gl.COMPILE_STATUS))
            throw new Error("compile: " + this.gl.getShaderInfoLog(shader));
        this.gl.attachShader(this.program, shader);
    }

    initTexture(index, tSampler, pixels) {
        const texture = this.gl.createTexture();
        this.gl.activeTexture(this.gl[`TEXTURE${index}`]);
        this.gl.bindTexture(this.gl.TEXTURE_2D, texture);

        this.gl.texParameteri(this.gl.TEXTURE_2D, this.gl.TEXTURE_MIN_FILTER, this.gl.LINEAR);
        this.gl.texParameteri(this.gl.TEXTURE_2D, this.gl.TEXTURE_MAG_FILTER, this.gl.NEAREST);

        this.gl.texImage2D(this.gl.TEXTURE_2D, 0, this.gl.RGBA, this.dimen, this.dimen, 0,
            this.gl.RGBA, this.gl.UNSIGNED_BYTE, pixels, 0);
        this.gl.uniform1i(this.getUniformLoc(tSampler), index);
    }

    initUniform(tUniform, value){
        const uniLoc = this.getUniformLoc(tUniform);
        this.gl.uniform1fv(uniLoc, value);
    }

    getAttribLoc(name) {
        let loc = this.gl.getAttribLocation(this.program, name);
        if (loc == -1) throw `getAttribLoc  ${name} error`;
        return loc;
    }

    getUniformLoc(name) {
        let loc = this.gl.getUniformLocation(this.program, name);
        if (loc == null) throw `getUniformLoc ${name} err`;
        return loc;
    }

    async loadRes(file) {
        const resp = await fetch(file);
        return resp.text();
    }

    render(){
        this.gl.drawArrays(this.gl.TRIANGLE_STRIP, 0, 4);
    }

    read() {
        let picBuf = new ArrayBuffer(this.dimen * this.dimen * 4);
        let picU8 = new Uint8Array(picBuf);
        let picU32 = new Uint32Array(picBuf);
        this.gl.readPixels(0, 0, this.dimen, this.dimen,
            this.gl.RGBA, this.gl.UNSIGNED_BYTE, picU8);
        return picU32
    }
}

1. 然后写一个基本的 `vertex shader`

v_shader.c 为啥要用.c做扩展名呢当然是因为方便代码高亮啊

这个shader和前面那个一模一样对画布的坐标进行了一个转化

#version 300 es

precision highp float;
precision highp int;

in vec4 g_pos;
out vec2 v_pos;

void main() {
    float curX = (g_pos.x + 1.) / 2.;
    float curY = (g_pos.y + 1.) / 2.;
    v_pos = vec2(curX, curY);
    
    gl_Position = g_pos;
}

2. 使用`uniform`的矩阵相乘

class MatrixUniform extends GPUComputing {
    async init(matrixA, matrixB) {
        await super.init("v_shader.c", "f_matrix_uniform.c");
        this.initUniform("i_matrixA", new Float32Array(matrixA));
        this.initUniform("i_matrixB", new Float32Array(matrixB));
    }
}

f_matrix_uniform.c:

#version 300 es

precision highp float;
precision highp int;

const int U_LENGTH = CANVAS_SIZE;

uniform float i_matrixA[U_LENGTH * U_LENGTH];
uniform float i_matrixB[U_LENGTH * U_LENGTH];

in vec2 v_pos;
out vec4 o_result;

vec4 int2rgba(const int i) {
    vec4 v4;
    v4.r = float(i >> 24 & 0xFF) / 255.;
    v4.g = float(i >> 16 & 0xFF) / 255.;
    v4.b = float(i >>  8 & 0xFF) / 255.;
    v4.a = float(i >>  0 & 0xFF) / 255.;
    return v4;
}

vec4 reverse(const vec4 v){
    return v.abgr;
}

int getValue(float matrix[U_LENGTH * U_LENGTH], int x, int y){
    return int(matrix[int(U_LENGTH) * x + y]);
}

void main() {
    // readPixels读取数值时次序与数组不一致, 
    int curX = int(float(U_LENGTH) * v_pos.y);
    int curY = int(float(U_LENGTH) * v_pos.x);

    int sum = 0;
    for (int i = 0; i < U_LENGTH; i++) {
        sum += getValue(i_matrixA, curX, i) * getValue(i_matrixB, i, curY);
    }

    o_result = reverse(int2rgba(sum));
}

数组传参是挺难看

3. 使用`Texture`的矩阵相乘

class MatrixTexture extends GPUComputing {
    async init(matrixA, matrixB) {
        await super.init("v_shader.c", "f_matrix_texture.c");
        this.initTexture(0, "samplerA", matrixA)
        this.initTexture(1, "samplerB", matrixB)
    }
}

f_matrix_texture.c:

#version 300 es

precision highp float;
precision highp int;

const int U_LENGTH = CANVAS_SIZE;
const float U_TEXTURE_POS_FIX = .5 / float(U_LENGTH);

in vec2 v_pos;
uniform sampler2D samplerA;
uniform sampler2D samplerB;

out vec4 o_result;

vec4 int2rgba(const int i) {
    vec4 v4;
    v4.r = float(i >> 24 & 0xFF) / 255.;
    v4.g = float(i >> 16 & 0xFF) / 255.;
    v4.b = float(i >>  8 & 0xFF) / 255.;
    v4.a = float(i >>  0 & 0xFF) / 255.;
    return v4;
}


int rgba2int(const vec4 v) {
    int r = int(v.r * 255.) << 24;
    int g = int(v.g * 255.) << 16;
    int b = int(v.b * 255.) << 8;
    int a = int(v.a * 255.) << 0;
    return r + g + b + a;
}

vec4 reverse(const vec4 v){
    return v.abgr;
}

int getMaxtrixValue(const sampler2D sampler, const float x, const float y){
    vec4 pixel = texture(sampler, vec2(x, y));
    return rgba2int(reverse(pixel));
}

void main() {
    int sum = 0;
    float textPos = 0.0;
    for (int i = 0; i < U_LENGTH; i++) {
        textPos = U_TEXTURE_POS_FIX + float(i) / float(U_LENGTH);
        sum += getMaxtrixValue(samplerA, v_pos.x, textPos) * getMaxtrixValue(samplerB, textPos, v_pos.y);
    }
    o_result = reverse(int2rgba(sum));
}

里面有个U_TEXTURE_POS_FIX常量用来修正texture取值的时候的位置以免取到像素边界上造成不必要麻烦

4. 然后咱们开始写个测试例子

先定义矩阵生成的函数和前面那篇博客差不太多只是把数据改用了Uint32Array来存放

function createMatrix(dims, fn) {
    let matrix = new Uint32Array(dims * dims);
    for (let i = 0; i < dims; i++) {
        for (let j = 0; j < dims; j++) {
            matrix[i * dims + j] = fn(i, j);
        }
    }
    return matrix;
}

然后定义一个执行函数

async function matrixJob(dimensions) {
    console.log("dimensions", dimensions);
    // 随机创建一个矩阵  然后转化成所需要的Uint8Array类型
    const randomMatrix = createMatrix(dimensions, () => Math.floor(Math.random() * 1000));
    const randomMatrixU8 = new Uint8Array(randomMatrix.buffer);
    console.log("intput matrix", randomMatrix);
    // console.log("intput matrix in Uint8Array", randomMatrixU8);
    let result = null;

    // 使用uniform进行传参
    console.time("demoMatrixUniform");
    const demoMatrixUniform = new MatrixUniform(dimensions);
    await demoMatrixUniform.init(randomMatrix, randomMatrix);
    demoMatrixUniform.render();
    result = demoMatrixUniform.read();
    console.timeEnd("demoMatrixUniform")
    // console.log("demoMatrixUniform output", result);


    // 使用texture进行传参
    console.time("demoMatrixTexture")
    const demoMatrixTexture = new MatrixTexture(dimensions);
    await demoMatrixTexture.init(randomMatrixU8, randomMatrixU8);
    demoMatrixTexture.render();
    result = demoMatrixTexture.read();
    console.timeEnd("demoMatrixTexture");
    // console.log("demoMatrixTexture output", result);

    
    // 为了对比 增加一个普通实现的矩阵相乘
    const matrixMultiplyCPU = function(ma, mb) {
        return createMatrix(dimensions, function(x, y) {
            let sum = 0;
            for (let i = 0; i < dimensions; i++) {
                sum += ma[x * dimensions + i] * mb[i * dimensions + y];
            }
            return sum;
        });
    }
    console.time("matrixMultiplyCPU");
    result = matrixMultiplyCPU(randomMatrix, randomMatrix);
    console.timeEnd("matrixMultiplyCPU");
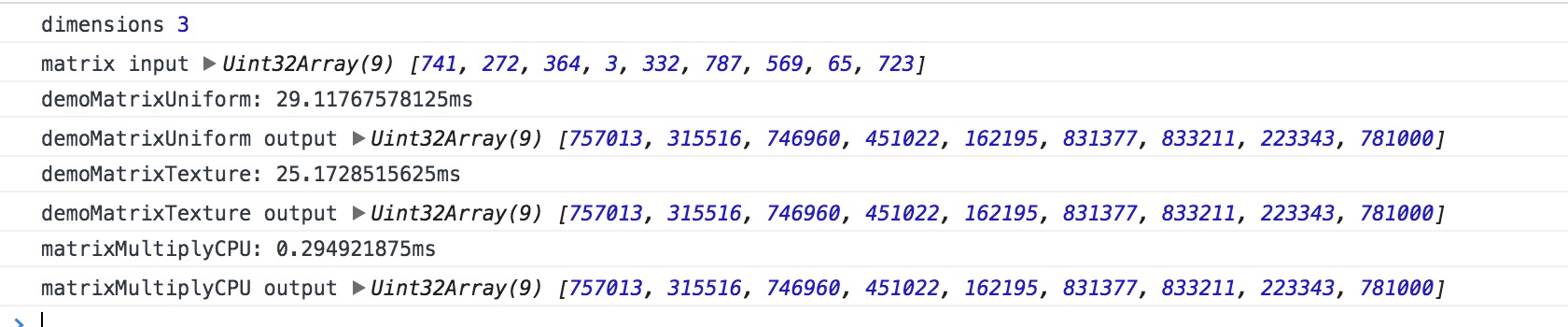
    // console.log("matrixMultiplyCPU output", result);
}

4. 结果分析

数据正确上没啥问题不过执行时间上很明显是直接计算来的快 uniform传参比texture略慢一点点

不过矩阵太小了看不出其他的所以咱们和前面一样使用多组数据进行对比因为受数组长度的限制所以之后的计算uniform方式就不参与进来比了

同样来一个多组的数据把不必要的log先注释掉

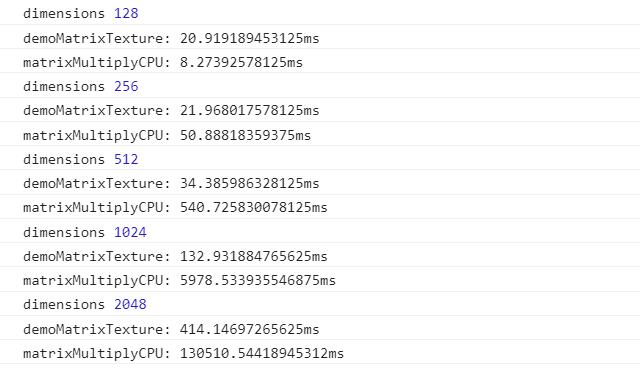
这个是一台设备

很明显纯WebGL计算比前面使用的gup.js耗时少20% 但是但是CPU计算在矩阵规模变大之后也有很大的下降不清楚具体是啥原因造成的应该是类型数组本身的性能有关吧

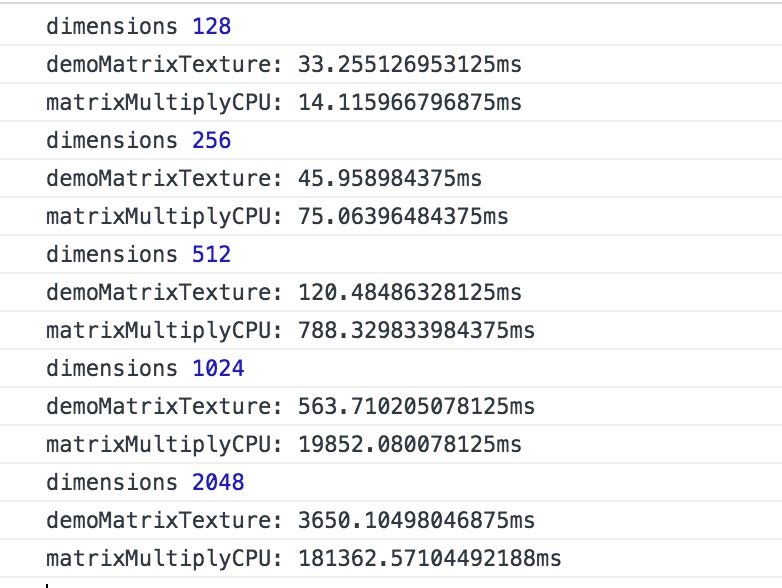
再看看那个配置GTX 1060 3G的电脑

这个就相当厉害了比gpu.js性能高了相当多特别是在维度低的时候即使是大小为2048 执行时间也减少了60+%

性能比原生数组CPU计算高了200倍比类型数组CPU计算高了300倍

但是前面也说了使用GPU计算最大的耗时在数据传输那如果数据传输不算真正计算有多快呢

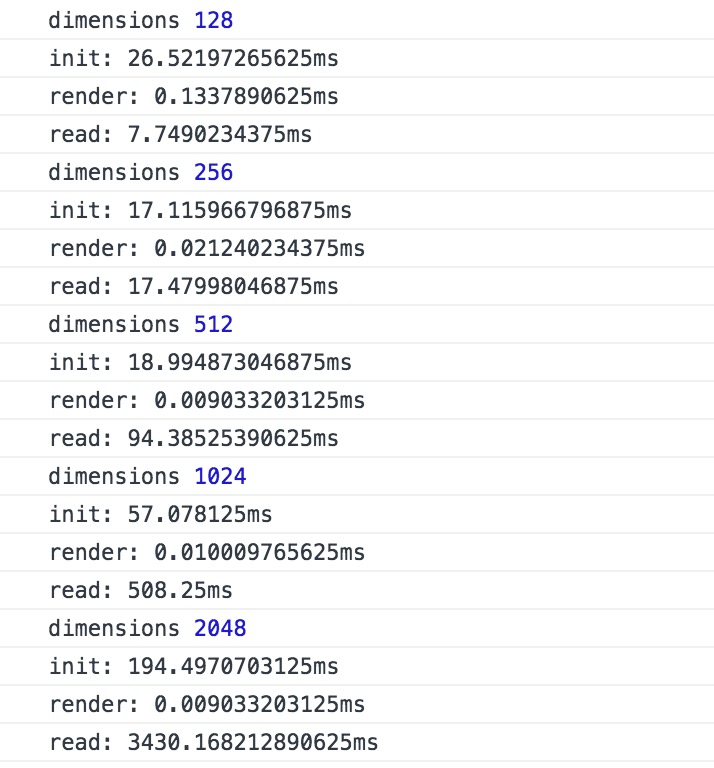
也是咱给几个上面的关键函数分别加个计时 init()和render()和read()分别计时

这个是低配的电脑

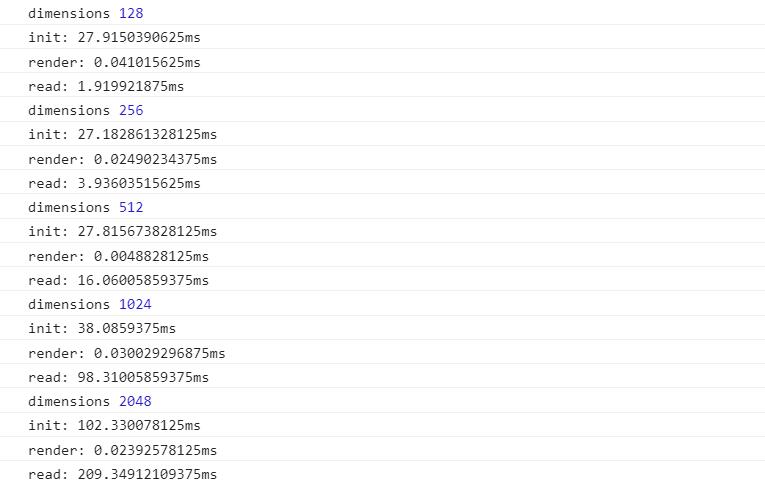
这个是1060的电脑

。。。。我觉得这个已经没法玩了啊

输入计算输出三者的耗时简直尤其是计算因为js计时器在毫秒级别是不准确的所以几乎可以忽略。。。 CPU和GPU差距有这么大吗按照纯计算的时间就算0.1毫秒计 i5和1060-O3G差的不止百万吧

两张显卡之间对比

输入的耗时差别不大最大也就两倍差距基本可以认为是一样的

但是读取耗时 1060比我渣核显低了最高有10倍

两个的计算时长都超过了js的计时精度所以没办法通过这样比较只能说不要用这种方法来比显卡计算性能

好了示例还有代码

代码包含了上面所有的代码示例因为考虑到大量的计算会造成浏览器卡死所以只保留了三个示例一个是按坐标距离设置透明度一个是将九像素纹理绘制到画布上还有一个是3维度的矩阵的乘法的三种实现以及分别的计时和结果

BLCL的博客小馆

js的GPU计算2之webgl
点击返回顶部

首页

关于

归档

js的GPU计算2之webgl

0.基本WebGL绘制

0.0 js中的流程就比较简单了

0.1 首先`vertex shader`:

0.2 然后就是`fragment shader`:

1.输入

1.0 粗暴的替换

1.1 使用 uniform 关键字

1.2 使用Texture 纹理

2. 输出

3. 矩阵乘法实验

0. 先是一个基本类

1. 然后写一个基本的 `vertex shader`

2. 使用`uniform`的矩阵相乘

3. 使用`Texture`的矩阵相乘

4. 然后咱们开始写个测试例子

4. 结果分析

js的GPU计算2之webgl

0.基本WebGL绘制

0.0 js中的流程就比较简单了

0.1 首先vertex shader:

0.2 然后就是fragment shader:

1.输入

1.0 粗暴的替换

1.1 使用 uniform 关键字

1.2 使用Texture 纹理

2. 输出

3. 矩阵乘法实验

0. 先是一个基本类

1. 然后写一个基本的 vertex shader

2. 使用uniform的矩阵相乘

3. 使用Texture的矩阵相乘

4. 然后咱们开始写个测试例子

4. 结果分析

0.1 首先`vertex shader`:

0.2 然后就是`fragment shader`:

1. 然后写一个基本的 `vertex shader`

2. 使用`uniform`的矩阵相乘

3. 使用`Texture`的矩阵相乘